(This page should be friendly to most colourblind viewers)
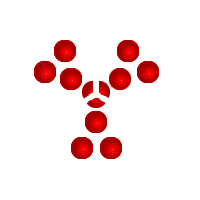
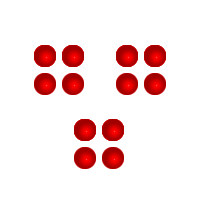
In this test, I attempt to convey the importance of symmetry. We start off with our sets arranged into a tightly packed circle. This allows for the highest chance of bi symmetry. We start off by making our first cut, then another, and another until we have no more wholes. You will see that dozenal lasts longer than decimal, proving that it is a balanced base.
|
Decimal
|
Dozenal
|
|
This is ten, all by itself, as you can see, no matter how you arrange it, ten never settles evenly unless you have 2 rows, but all even bases share this. This particular arrangement is best for fitting in a circle.
|
This is a dozen, the even arrangement is easy to achieve, this is the best arrangement for fitting
within a circle. |
Translation Symmetry
This tests whether each set can fall 1 row down without finding any gaps. If it gains or loses any units, it fails. This is incredible useful for shipping companies and is one of the reasons you usually will find a dozen eggs as opposed to ten. With ten eggs, you have less ways that you can stack them.
|
Decimal
|
Dozenal
|
As I summarize on the introduction page:
If we have a 2 x 5 egg carton and we try to square it off by adding another box parallel to it, we end up with 4x5. Well, that's not square, so we do it once more, 6x5. Nope, it's not going to work. If we try any other number of rows than 2 or 5, they wont add up to 10:
2 x 5 = 10 good
3 x 3 = 9 too low
3 x 4 = 12 too high
4 x 2 = 8 too low
4 x 3 = 12 too high
5 x 2 = 10 good
Now we try a typical 2x6 egg carton, trying to square it off, we add another 2 boxes and we have a perfect 6x6. Now we can store this in trucks easily, we can stack them without having a layered brick pattern. We can stack them in 3 rows of 2x6 egg cartons, easily counted from a distance too. Look at all the ways we can order them:
2 x 6 = 12 good
3 x 4 = 12 good
4 x 3 = 12 good
6 x 2 = 12 good
If we have a 2 x 5 egg carton and we try to square it off by adding another box parallel to it, we end up with 4x5. Well, that's not square, so we do it once more, 6x5. Nope, it's not going to work. If we try any other number of rows than 2 or 5, they wont add up to 10:
2 x 5 = 10 good
3 x 3 = 9 too low
3 x 4 = 12 too high
4 x 2 = 8 too low
4 x 3 = 12 too high
5 x 2 = 10 good
Now we try a typical 2x6 egg carton, trying to square it off, we add another 2 boxes and we have a perfect 6x6. Now we can store this in trucks easily, we can stack them without having a layered brick pattern. We can stack them in 3 rows of 2x6 egg cartons, easily counted from a distance too. Look at all the ways we can order them:
2 x 6 = 12 good
3 x 4 = 12 good
4 x 3 = 12 good
6 x 2 = 12 good
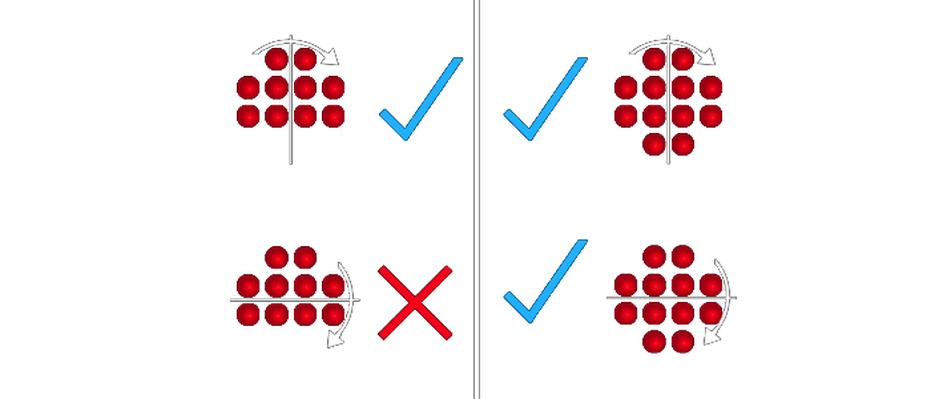
Reflective Symmetry
This is not as important as the other tests, but it shows off how much of a balanced base this is.
|
Decimal
|
Dozenal
|