(This page should be friendly to most colourblind viewers)
This is one of the biggest reasons people say, "I don't want to do math, it's too much work."
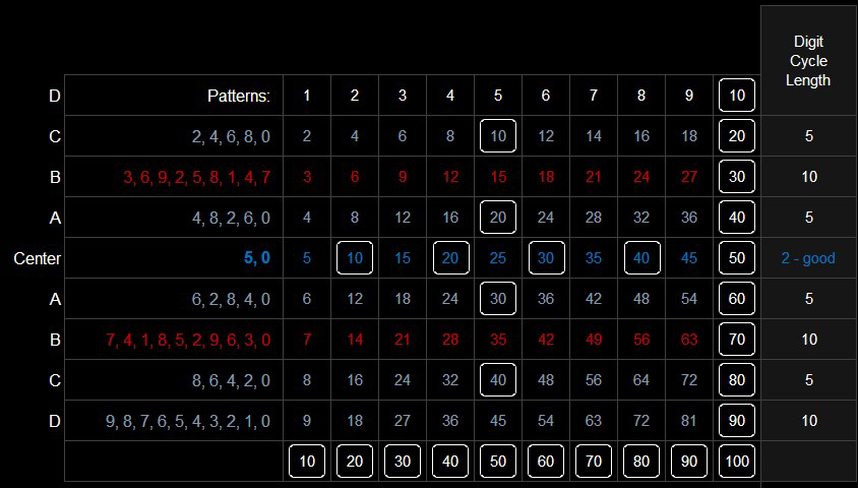
We all find ourselves cowering behind the mighty 5 saying, "2.4? Okay, that's close enough, let's round it to 2.5." Contrast this to the dozenal multiplication chart, we find many patterns and less rules to remember.
We all find ourselves cowering behind the mighty 5 saying, "2.4? Okay, that's close enough, let's round it to 2.5." Contrast this to the dozenal multiplication chart, we find many patterns and less rules to remember.
|
Decimal
|
But first, let's take a look at our decimal multiplication table:
|
The squares show the zero enders. These squares reflect a healthy and easy number system. Hmm...
Notice the big open areas without zero enders in the 4 corners of the grid. All of those numbers, you'll have to memorize in your times tables.
Notice the big open areas without zero enders in the 4 corners of the grid. All of those numbers, you'll have to memorize in your times tables.
|
Now, let's take a look at the dozenal multiplication table:
|
Dozenal
|
With all these zero enders, the sequences are straight forward. You can feel confident in your multiplication that takes just seconds to double check.
|
Those 5's and 7's are a pain sure, but when you can take a number like 64, 49, or 36 and multiply that with ease, you'll wonder why we still use the decimal system.
* read 7's even trick is below. |
Tricks to Use Instead
of Memorizing Tables
|
Digit Behavior
In our decimal system, it's very often that you'll look at a number like 51 and think, "gee, that looks prime, but it might not be." But as it turns out, 51 is not prime; It's divisible by 3 and 17. Another problem is that we find it hard to tell what a number can be divided by.
In dozenal, we can look at a number like 63 and immediately know that it is divisible by 3 without a doubt. The only thing we can say in decimal is that something is divisible by 2 or 5. On the flip side, this also means that dozenal numbers that end in 1, 5, 7, or Ƹ, many of them are prime. Take a look at this chart I made and see what I mean: As we see above, if it ends in, 2, 3, 4, 6, 8, 9, ᕍ, or 0, we know for a fact that is is not prime.
In this next section, I talk about the tricks with each digit on the multiplication table. As you read ahead here, I get the feeling that if this was taught to children, they would learn their tables much faster than in decimal. In decimal, there are a few tricks here and there, but it's mostly up to memorization.
Before reading, keep in mind:
Blue is right hand. These are our ones. Red is left hand. These are our dozens 6's (Easiest)
In this example, 6 x 4
What is half of your multiplier? 2 Move the radix point over to the right. 20 Example 2: 6 x 7 What is half of your multiplier? 3.6 (6 is half of our base) Move the radix point over to the right. 36 7 evens (Easy if even)
4's and 8's (Easy)
In this example, 4 x 9
Count your fingers using this pattern: "4, 8, 0". Every time you say, "zero", close your fist. Every time you reach zero, count a finger on your left hand (that's your dozens). Keep counting until you reach your multiplier: 4, 8, 0; 4, 8, 0; 4, 8, 0; You have 3 sets on your left hand. Your right hand landed on a 0. Our result is 30. ------------------------------------------------------- In this example, 8 x 5 Count your fingers using this pattern: "8, 4, 0". Every time you say, "zero", close your fist. Start with 1 in your left hand (our multiplier is more than 8). Every time you reach "four" or "zero", add one to your left hand. Keep counting until you reach your multiplier: 8, 4, 0; 8, 4- Your right hand landed on a 4. Our result is 34. 3's and 9's (Easy)
In this example, 3 x 7
Count your fingers using this pattern: "3, 6, 9, 0". Every time you say, "zero", close your fist. Every time you reach zero, count a finger on your left hand (that's your dozens). Keep counting until you reach your multiplier: 3, 6, 9, 0; 3, 6, 9. You have 1 set on your left hand. Your right hand landed on a 9. Our result is 19. ------------------------------------------------------- In this example, 9 x 5 Count your fingers using this pattern: "9, 6, 3, 0". Every time you say, "zero", close your fist. Start with 1 in your left hand (our multiplier is 9, not 3). Every time you reach "six," "three," and "zero", count a finger on your left hand. Keep counting until you reach your multiplier 9, 6, 3, 0; 9. Your right hand landed on a 9. Our result is 39. Ƹ's (Same as in all even bases)
5 evens (The hard one)
|