(This page should be friendly to most colourblind viewers)
|
Decimal
|
Dozenal
|
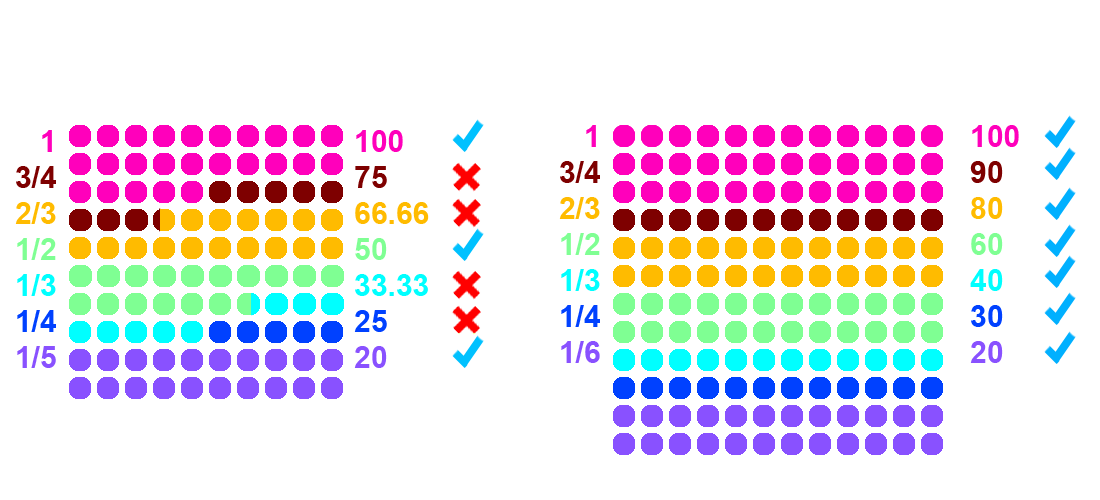
This is a diagram of percentages between both base ten and twelve. If you look at the partitions on the right, you'll notice they are in neat rows, while on the left, you'll see they are staggered. Why do the divisions in base twelve have straight rows? Are the partitions falsely represented? Surprisingly no.
Base 12 simply excels in dividing by quarters, thirds, and sixths.
Unfortunately for base ten, only dividing by 2 and 5 can give you those clean numbers.
Base 12 simply excels in dividing by quarters, thirds, and sixths.
Unfortunately for base ten, only dividing by 2 and 5 can give you those clean numbers.
Well then, can’t we start using fifths? How common are fifths? And for that matter, how can you cut a cake into fifths accurately? When you cut with a knife evenly, you dissect, creating 2 parts each time. Unfortunately, 5 is an odd number. So, as you can imagine, if you start cutting a cake:
first cut = 2 parts
second cut = 4 parts
third cut = 6 parts
This is one of the big problems, 5 being an odd number, it creates a less useful number to work with. People like the number 5 because it's a nice number to multiply, since its numbers end in either 0 or 5, it’s easy to memorize (5,10,15,20,25,...). But did you know all even bases have a numeral that can do this? For the dozenal system it's 6, the product always ends in 0 or 6 (6,10,16,20,26,30...). However, it comes with advantages, since 6 is even, 6 can be split again into halves or thirds.
5 is prime, therefore, it cannot divide further (evenly).
first cut = 2 parts
second cut = 4 parts
third cut = 6 parts
This is one of the big problems, 5 being an odd number, it creates a less useful number to work with. People like the number 5 because it's a nice number to multiply, since its numbers end in either 0 or 5, it’s easy to memorize (5,10,15,20,25,...). But did you know all even bases have a numeral that can do this? For the dozenal system it's 6, the product always ends in 0 or 6 (6,10,16,20,26,30...). However, it comes with advantages, since 6 is even, 6 can be split again into halves or thirds.
5 is prime, therefore, it cannot divide further (evenly).
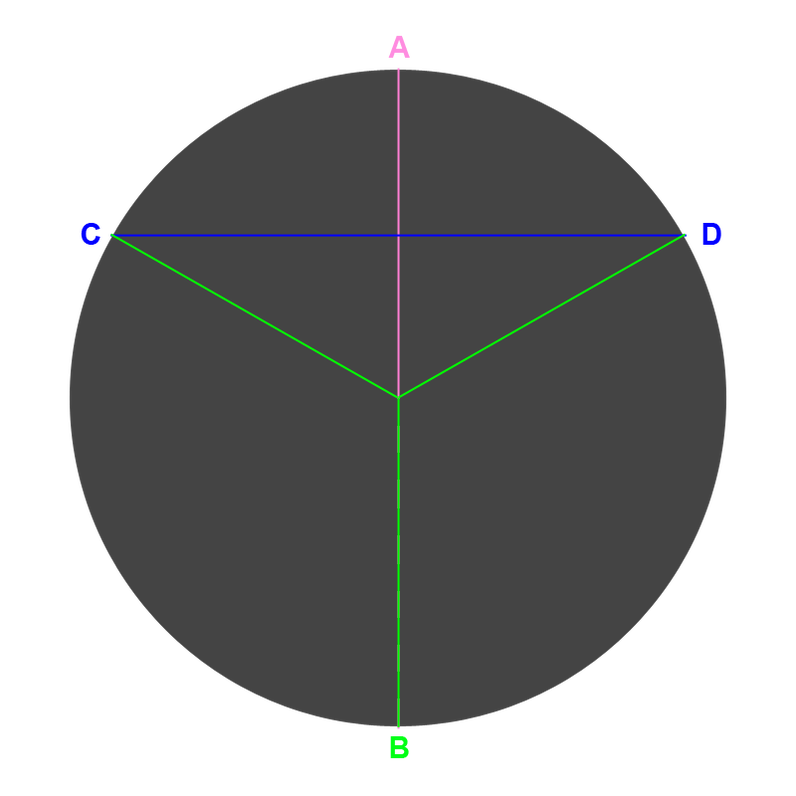
You might ask yourself, why would I want thirds? What good are they? Thirds are useful in dozenal as they fit into 10 evenly. We can combine 3 with 9 and make 10. So now that we respect them, how do we represent them in the real world without making a mess? Let's imagine a pie, we want to make 3 equal slices without making extra cuts.
- Measure the longest distance across the pie, label it A and B
- Halfway between A and B is your center.
- Halfway between the center and A, measure perpendicular in both directions, until you reach the edge of the pie.
- Label the points that touch the sides of the pie, C and D.
- From C to the center, make a cut.
- From D to the center, make a cut.
- From B to the center, make a cut.
You just made 3 perfect slices of pie even though it was an odd number. Although trying to do that with 5 will be pretty difficult, and will take longer.
- Measure the longest distance across the pie, label it A and B
- Halfway between A and B is your center.
- Halfway between the center and A, measure perpendicular in both directions, until you reach the edge of the pie.
- Label the points that touch the sides of the pie, C and D.
- From C to the center, make a cut.
- From D to the center, make a cut.
- From B to the center, make a cut.
You just made 3 perfect slices of pie even though it was an odd number. Although trying to do that with 5 will be pretty difficult, and will take longer.
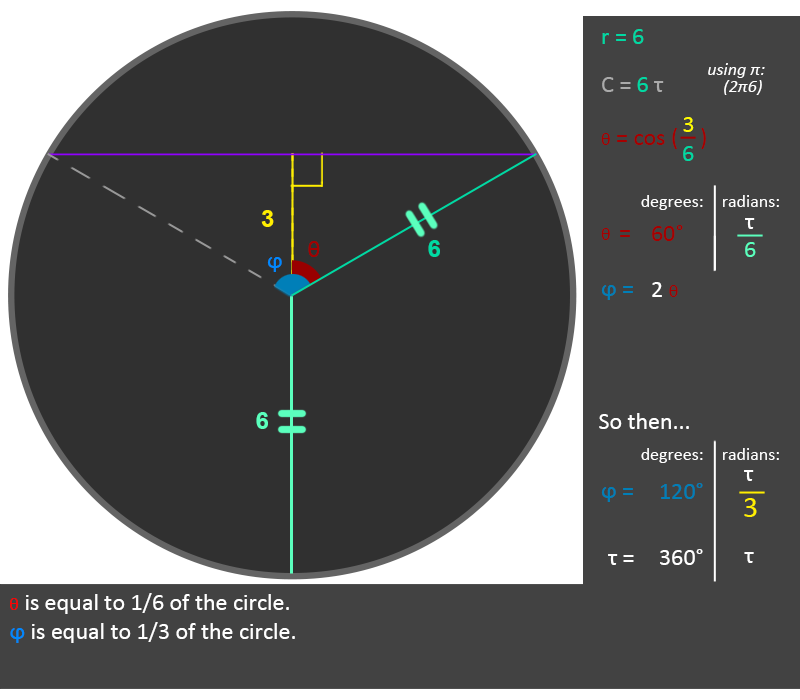
There's some interesting trigonometry behind it all. In the following example, I show both radians and degrees. Keep in mind that I use the Tau instead of Pi for the radians. For this operation, Tau is far more effective and clear (although in some other fields, I find π useful).
Because the partitions in dozenal are are nice zeroed numbers, (20,30,40,60,80,90,100), it is very easy to work with them. Imagine reading them on a measuring cup! 1000mL divides up nice and tidy:
|
Most common:
3/4 = 900mL 2/3 = 800mL 1/2 = 600mL 1/3 = 400mL 1/4 = 300mL Sixths:
5/6 = ᕍ00mL 4/6 = 800mL 3/6 = 600mL 2/6 = 400mL 1/6 = 200mL |
Eighths:
7/8 = ᕍ60mL 6/8 = 900mL 5/8 = 760mL 4/8 = 600mL 3/8 = 460mL 2/8 = 300mL 1/8 = 160mL |
Ninths:
8/9 = ᕍ80mL 7/9 = 940mL 6/9 = 800mL 5/9 = 680mL 4/9 = 540mL 3/9 = 400mL 2/9 = 280mL 1/9 = 140mL |
Do-fourths:
13/14 = Ƹ30mL 12/14 = ᕍ60mL 11/14 = 990mL 10/14 = 900mL Ƹ/14 = 830mL ᕍ/14 = 760mL 9/14 = 690mL |
8/14 = 600mL
7/14 = 530mL 6/14 = 460mL 5/14 = 390mL 4/14 = 300mL 3/14 = 230mL 2/14 = 160mL 1/14 = 90mL |
As you can see, not even once have we seen digits exceed 2 placements. If we were to convert these to Litres, we would get numbers like 3;9 L , but never 3;94 L .
Now, let's take a look at the decimal equivalent. Notice here what we have to deal with:
- 4 different digit behaviours on common fractions
- 4 different digit behaviours on the eighths
- 9 different behaviours for ninths (why ninths? As an extension of thirds)
- 8 different behaviours for the sixteenths
- 4 different digit behaviours on common fractions
- 4 different digit behaviours on the eighths
- 9 different behaviours for ninths (why ninths? As an extension of thirds)
- 8 different behaviours for the sixteenths
|
Most common:
3/4 = 750mL 2/3 = 666.666... mL 1/2 = 500mL 1/3 = 333.333... mL 1/4 = 250mL 1/5 = 200mL Fifths:
4/5 = 800mL 3/5 = 600mL 2/5 = 400mL 1/5 = 200mL |
Eighths:
7/8 = 875mL 6/8 = 750mL 5/8 = 625mL 4/8 = 500mL 3/8 = 375mL 2/8 = 250mL 1/8 = 125mL |
Ninths:
8/9 = 888,888...mL 7/9 = 777.777...mL 6/9 = 666.666...mL 5/9 = 555.555...mL 4/9 = 444.444...mL 3/9 = 333.333...mL 2/9 = 222.222...mL 1/9 = 111.111...mL |
Sixteenths:
15/16 = 937.5mL 14/16 = 875mL 13/16 = 812.5mL 12/16 = 750mL 11/16 = 687.5mL 10/16 = 625mL 9/16 = 562.5mL |
8/16 = 500mL
7/16 = 437.5mL 6/16 = 375mL 5/16 = 312.5mL 4/16 = 250mL 3/16 = 187.5mL 2/16 = 125mL 1/16 = 62.5mL |
|
Fifths are okay, but they are rarely used since 5 is not even.
To visualize, imagine how hard it is to cut a pie in fifths. |